Innovative positioning methodologies in brand strategy have evolved to incorporate advanced data analytics, artificial intelligence, and neuroscientific approaches.
One cutting-edge technique uses machine learning algorithms to analyze vast consumer data and identify micro-segments for hyper-targeted positioning. This approach, known as algorithmic positioning, utilizes clustering algorithms (e.g., k-means, DBSCAN) and neural networks to uncover latent consumer behaviour and preference patterns.
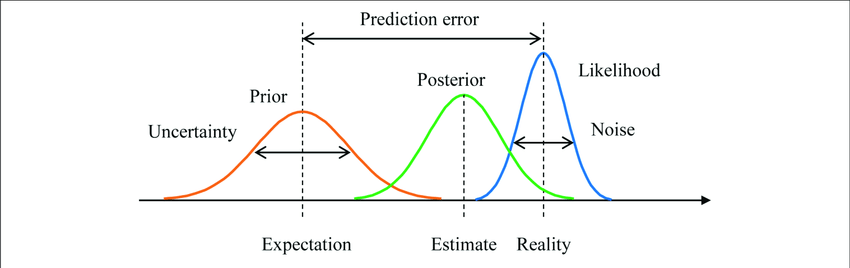
Another innovative methodology is neuromarketing-based positioning, which leverages neuroimaging techniques like fMRI and EEG to measure consumers’ subconscious responses to brand stimuli.
This approach can be mathematically represented using the Engagement-Power-Frustration (EPF) model:
$$E = \alpha P – \beta F$$
E is engagement, P is power (approach motivation), F is frustration (avoidance motivation), and α and β are weighting coefficients.
By optimizing this equation, brands can fine-tune their positioning to maximize emotional engagement and minimize cognitive dissonance.
Additionally, real-time adaptive positioning systems are emerging, utilizing IoT devices and edge computing to adjust brand messaging based on contextual factors dynamically.
These systems employ Bayesian inference models to update positioning strategies, represented as continuously
$$P(θ|x) = \frac{P(x|θ)P(θ)}{P(x)}$$
θ represents the positioning parameters, and x is the observed consumer data.
This approach allows for unprecedented agility in brand positioning, allowing brands to adapt to rapidly changing market conditions and consumer sentiments.
Contents
Brand Positioning vs. Sphere Positioning
While brand and sphere positioning share the term “positioning,” they operate in fundamentally different domains.
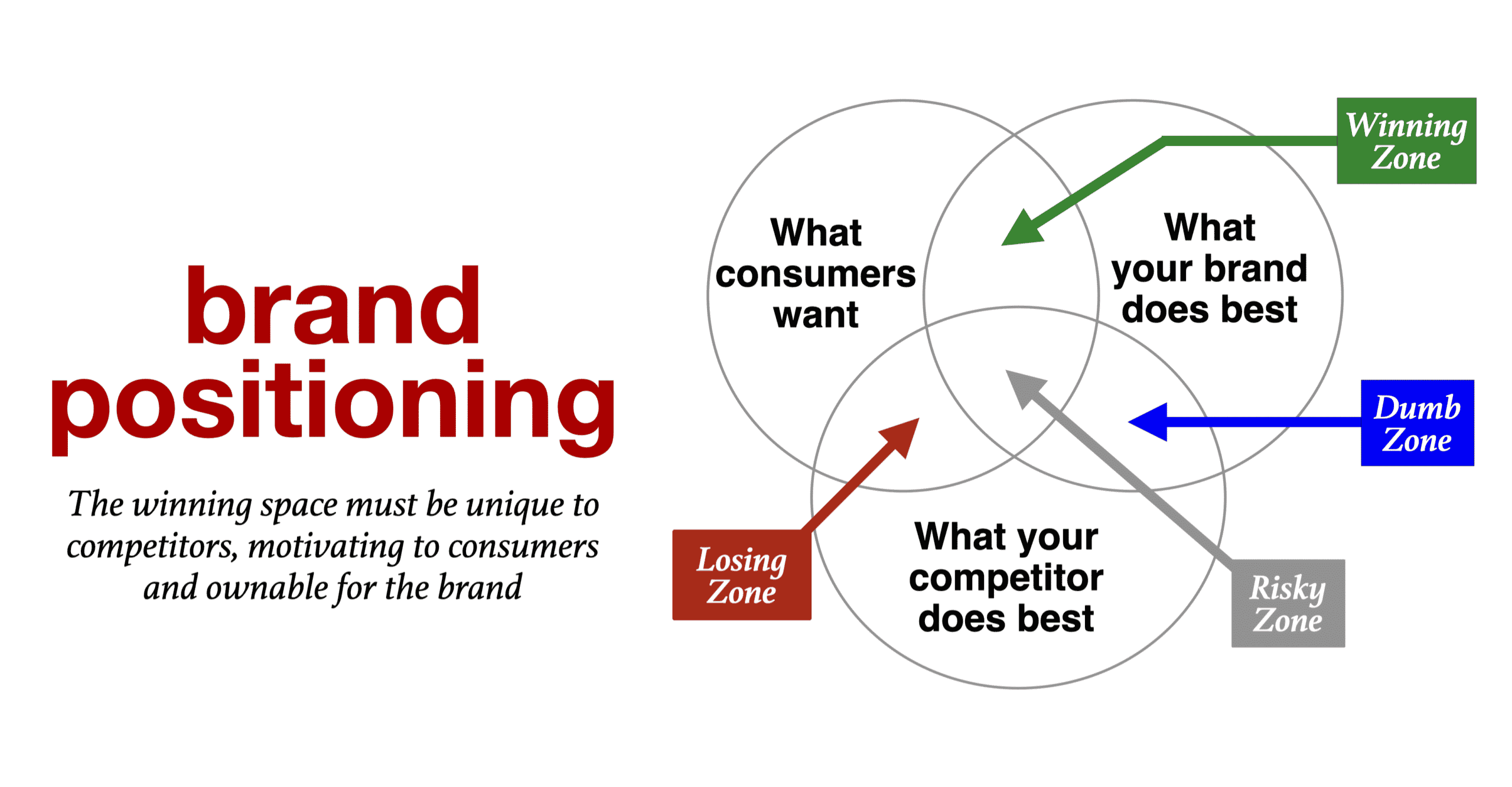
Brand positioning is a strategic marketing concept focused on creating a unique perception of a brand in consumers’ minds. It involves defining a brand’s value proposition, target audience, and competitive advantage to differentiate it from competitors.
In contrast, as Unity’s Visual Effect Graph exemplifies, sphere positioning in computer graphics is a technical process for calculating and manipulating particle positions within a spherical volume.
The key distinction lies in their applications and methodologies.
Brand positioning influences perceptions through market research, consumer psychology, and communication strategies. It’s expressed through marketing messages, visual identity, and customer experiences. On the other hand, Sphere positioning employs mathematical algorithms and computer graphics techniques to distribute particles in 3D space, often using parameters like surface, volume, and thickness to achieve desired visual effects.
While brand positioning aims to create emotional and cognitive associations, sphere positioning focuses on precise spatial calculations to generate visual representations.
Sphere Positioning in Machine Vision Systems
Sphere positioning in machine vision systems has emerged as a precise and flexible method for accurate object localization and measurement. By leveraging the geometric properties of spheres, these systems can accurately determine spatial coordinates using single or multiple camera views. One approach utilizes a multi-sphere artefact with an edge-based vision measurement system to extract sphere information and derive coordinate data. This technique employs new measurement models to enhance precision. Another method explores a novel geometric constraint for single-view sphere positioning, which can be particularly useful in scenarios where multiple camera setups are impractical. The accuracy of sphere positioning can be further improved through stereo camera systems, which provide depth information and enable more robust 3D reconstruction. Advanced algorithms have also been developed to automatically estimate sphere centres from calibrated camera images, combining ellipse detection and spatial localization techniques to streamline the process. These approaches collectively contribute to advancing machine vision systems in industrial automation, quality control, and metrology applications.
Advanced Sphere Mapping Strategies
Sphere mapping is a powerful technique in computer graphics for creating realistic reflections and environment maps. While traditional sphere mapping methods can introduce distortions, several advanced strategies have been developed to improve accuracy and efficiency.
One notable approach is the HEALPix (Hierarchical Equal Area isoLatitude Pixelization) method, which partitions the sphere into equal-area quadrilateral elements. This technique allows fast integration over the sphere and is particularly useful for environment sampling. HEALPix provides a near-equal solid-angle property, ensuring uniform sampling across the sphere’s surface.
Another advanced strategy involves subdividing the sphere using a set of simple equations that fit naturally into the six-face cube structure. This approach samples the sphere more evenly than traditional cube maps while leveraging hardware optimizations designed for cube map texturing. The result is a more balanced sampling of the sphere that can be efficiently implemented in real-time graphics applications.
A third method employs a family of skewed great circles as the subdivision strategy, resulting in similarly distorted texels across the sphere. This approach can provide consistent visual quality when applied to environment mapping or other spherical projection tasks.
For cortical surface mapping, crucial in neuroimaging, advanced techniques have been developed to achieve near-isometric mapping of complex brain geometries onto spheres. One method employs deep learning, specifically using a Spherical U-Net model on icosahedron discretized spheres. This approach learns high-level geometric features from the original surface mesh to predict a diffeomorphic deformation field, effectively moving each vertex on the spherical mesh to its optimal position. The process can be expressed mathematically as:
$$S_1 = S_0 \circ \phi_0$$
where $$S_1$$ is the optimized spherical mesh, $$S_0$$ is the initial spherical mesh, and $$\phi_0$$ is the predicted deformation field[2].
A coarse-to-fine multi-resolution framework can be employed to handle large nonuniform distortions. This iterative process can be represented as:
$$S_{t+1} = S_t \circ \phi_t$$
with progressively increased resolution until the final $$S_t$$ reaches an acceptable level of distortion.
In computer graphics applications, sphere mapping can be enhanced using texture matrices for hardware-accelerated environment mapping. This technique allows for dynamic updates to the environment map without requiring per-vertex calculations. The process involves manipulating the texture matrix to adjust the sphere map’s orientation based on the view direction, enabling efficient real-time reflections.
These advanced sphere mapping strategies offer improved accuracy, efficiency, and flexibility compared to traditional methods, making them valuable tools in various fields, including computer graphics, neuroimaging, and scientific visualization.
Comparative Analysis: Brand vs. Sphere
A comparative analysis of brand and sphere positioning reveals distinct methodologies, applications, and objectives despite their shared use of “positioning.”
Brand positioning operates within the realm of marketing strategy, focusing on creating a unique perception of a brand in consumers’ minds. This process involves:
1. Target audience identification
2. Value proposition development
3. Competitive differentiation
4. Communication strategy formulation
Brand positioning effectiveness is measured through brand awareness, customer loyalty, and market share metrics. It relies heavily on qualitative data, consumer psychology, and market research to shape brand perception.
In contrast, sphere positioning in computer graphics and visual effects is a technical process for calculating and manipulating particle positions within a spherical volume. Key aspects include:
1. Mathematical algorithms for spatial distribution
2. Parameter control (e.g., surface, volume, thickness)
3. Integration with graphics engines (e.g., Unity’s Visual Effect Graph)
4. Real-time rendering and performance optimization
Sphere positioning effectiveness is evaluated through visual fidelity, computational efficiency, and the ability to achieve desired visual effects. It relies on quantitative data and precise calculations[existing_sections].
The fundamental differences can be summarized in the following comparative table:
While brand positioning aims to create lasting emotional and cognitive associations, sphere positioning focuses on generating precise, often dynamic, visual representations. The former deals with abstract concepts and human psychology, while the latter manipulates concrete spatial data.
Regarding technological application, sphere positioning has found utility beyond computer graphics. In machine vision systems, for instance, sphere positioning techniques are used for accurate object localization and measurement. These systems leverage the geometric properties of spheres to determine spatial coordinates with high precision, often using single or multiple camera views.
The mathematical foundations of sphere positioning can be expressed using equations such as:
$$P = C + r(\sin\theta\cos\phi, \sin\theta\sin\phi, \cos\theta)$$
Where $$P$$ is the position of a point on the sphere, $$C$$ is the centre of the sphere, $$r$$ is the radius, and $$\theta$$ and $$\phi$$ are the polar and azimuthal angles, respectively.
In contrast, brand positioning often relies on more abstract models, such as perceptual mapping, which can be represented mathematically but lacks the precise spatial definition of sphere positioning.
Advanced sphere mapping strategies, such as HEALPix (Hierarchical Equal Area isoLatitude Pixelization), further differentiate the technical sophistication of sphere positioning from the more conceptual nature of brand positioning. These strategies allow uniform sampling across a sphere’s surface, which is crucial for applications in computer graphics and scientific visualization.
In conclusion, while brand and sphere positioning share the concept of “positioning,” they represent fundamentally different approaches applied in distinct fields. Brand positioning is a strategic marketing tool focused on shaping perceptions, while sphere positioning is a technical process for precise spatial calculations and representations.
Brand Positioning Case Studies
1. Netflix’s Algorithmic Content Positioning:
Netflix employs sophisticated machine learning algorithms to analyze the viewing patterns and preferences of its 200+ million subscribers. This data-driven approach allows for hyper-personalized content recommendations and positioning. The company uses collaborative filtering and matrix factorization techniques, which can be represented mathematically as:
$$R_{ui} = \mu + b_u + b_i + q_i^T p_u$$
Where R_{ui} is the predicted rating for the user you on item I, μ is the overall average rating, b_u and b_i are user and item biases, and q_i and p_u are latent factor vectors for items and users, respectively.
2. Coca-Cola’s Neuromarketing-Based Positioning:
Coca-Cola utilized EEG and eye-tracking technologies to optimize its “Taste the Feeling” campaign. They refined their positioning by measuring neural responses to various ad elements to evoke stronger positive emotions. The analysis involved quantifying attention and emotional valence using metrics like the Frontal Alpha Asymmetry (FAA) index:
$$FAA = \ln(α_{right}) – \ln(α_{left})$$
Where α represents alpha band power in the respective hemispheres.
Computer Graphics Case Studies:
1. Pixar’s RenderMan Sphere Tracing:
Pixar’s RenderMan software uses advanced sphere tracing techniques for efficient ray marching in complex scenes. This method, known as Enhanced Sphere Tracing (EST), improves upon traditional sphere tracing by adaptively adjusting step sizes. The core algorithm can be expressed as:
$$p_{n+1} = p_n + \min(f(p_n), \frac{f(p_n)^2}{2|∇f(p_n)|})n$$
Where p_n is the current position, f(p_n) is the signed distance function, and n is the normalized ray direction.
2. Unity’s Visual Effect Graph Sphere Positioning:
Unity’s Visual Effect Graph employs sophisticated sphere positioning techniques for particle systems. One notable application is in the creation of realistic galaxy simulations. The positioning of stars within a galactic sphere uses a modified version of the Hernquist profile:
$$ρ(r) = \frac{M}{2πa^3} \frac{1}{(r/a)(1+r/a)^3}$$
Where ρ(r) is the density at radius r, M is the total mass, and a is a scale radius. This distribution is then sampled using inverse transform sampling to position particles within the galactic sphere[4].
3. Nvidia’s RTX Sphere Tracing for Real-Time Global Illumination:
Nvidia’s RTX technology utilizes sphere tracing for real-time ray tracing and global illumination. Their approach combines traditional sphere tracing with machine learning-accelerated denoising. The core algorithm is enhanced by a neural network that predicts optimal ray termination conditions, significantly reducing the number of iterations required. This hybrid approach can be represented as:
$$t_{n+1} = t_n + \max(d_{min}, f(p(t_n)) \cdot (1 – α_{NN}(p(t_n), n)))$$
Where t_n is the current ray distance, f(p(t_n)) is the signed distance function, and α_{NN} is a neural network that predicts a scaling factor based on the current position and ray direction.
These case studies demonstrate how advanced positioning techniques are applied in brand strategy and computer graphics. Brand positioning uses data and neuroscience to create more targeted and emotionally resonant messaging. CG emphasises developing more efficient and realistic rendering techniques, often combining traditional algorithms with machine learning approaches to push the boundaries of visual fidelity and performance.